简单的问题容易解决，复杂的问题难解决。

解决复杂问题的常用方式就是将复杂问题转换为简单问题再解决。

我们从研究查字典开始，研究下查询算法的特征要点。

1.查字典

简单问题和复杂问题如何区分呢？我们以查字典为例考察下。

新华字典是陪伴我们学习汉字常用的工具书，据网上资料，最新版本的新华字典收录汉字11700个(为了简化场景，仅关注收录的单字，不包括对字的解释)。

新华字典使用了多种编码方式，常用的有页码编码、拼音首字母编码。我们计算下这两个索引维度和汉字的信息量。

信息熵是度量信息量的概念，我们使用信息熵计算结果如下：

类型集合特征信息熵拼音26个拼音字母4.7页码689页9.42汉字11700个单字13.5

我们的最终目标是找到某个汉字，如果直接通过汉字查找，就是在11700个汉字中查找，信息复杂度为13.5，直观上我们就知道这个复杂度很高。

我们最常用的是用拼音查找，知道第一个首字母就能将汉字搜索范围降下来，第二个字母继续下降，最终通过拼音可以高效的找到需要的汉字。

我们参照使用字典的过程，可以推演查询算法的主要步骤。

2.编码

原始信息需要经过分类才能更高效的取用，此处编码不是简单的替换符号，还要更高效的凝聚信息。

2.1.编码的作用

非加密场景编码的重要作用是：信息压缩。

编码前信息如果是用11700个元素组成，添加编码信息后使用的信息元素要下降，比如用拼音排序就可以将这11700个元素分成26个组，每次筛选时，就可以快速定位到组内查询，可以极大降低查询的动作数量。

这里新增的信息压缩维度的数据类似于字典索引的功能。设想给你一本没有编码的字典，字典的11700个汉字随机的分布，使用这样的字典查找数据效率是何等的低，简直就是一个噩梦。

2.2.编码原则

字典编码的重要原则包括：

• 正交化

• 顺序化

2.2.1.正交化

正交化就是多个维度的信息不能有交叉，只有将数据维度拆分成，完全正交的特征空间才符合最优的编码原则。

我们使用的直角坐标系、经纬度坐标系就符合正交化的原则。

正交化与奥卡姆剃刀原则的“如无必要，勿增实体”的要求是一致的。

2.2.2.顺序化

顺序化的特征就是多个元素之间前后属性是确定的，局部中隐含着全局的信息。比如：

• 1-10的序列，4一定在5的左边，6一定在5的右边。

• a-z的序列，g一定在h的左边，i一定在h的右边。

顺序化的信息，计算机都可以编码成数字，通过序号的顺序性，可以递归将数据分组，快速定位目标数据的位置。二分法充分发挥了顺序化的特性，是目前速度最快的查找算法。

3.查找

走到查找流程，我们可以认为数据的编码任务已经完成，现在需要从这些数据中捞取对我们有价值的数据。

查找动作不仅在计算机中，比如捕鱼、以及勘探资源都是这里的查找。

 大家完全可以将查找的动作从计算机的查找中走出来，用计算机算法的视角观察身边需要查找的事情。

生活阅历是理解计算机算法，最直观的认知资源宝库。

3.1.起始位置

开始查找第一步，决定起始位置。

3.1.1.从第一个或最后一个位置开始

现实生活：

刚开始学习查字典的时候，对字典还不熟悉，肯定会先打开索引页，按照拼音找到对应的汉字，然后再翻到页码指引的位置。这个严格来说，只是第一步是从第一个位置开始的。

计算机算法：

计算机算法的第一个位置开始，就是写一个for循环，从第一个元素依次查找。如果数据量巨大该算法花费的时间越来越长。

3.1.2.从中间位置开始

现实生活：

当对字典越来越熟悉时，打开书口，快速定位拼音首字母所在位置。

计算机算法：

字典的例子是已经完成了顺序编码，计算机算法如果没有实现按顺序存储，就无法使用该方式。

如果计算机访问的是数据已经排序，计算机可以通过二分法，直接访问中间的数据，就可以根据中间值的信息和顺序确定目标数据分布在中间值的左侧还是右侧。通过递归，可以用相对于“从第一个位置开始查找”花费更少的步骤找到目标数据。

3.1.3.随机开始

如果数据量巨大，使用从初始位置访问花费的时间超出了合理的时间，比如要花费20年，则不能使用起始位置访问法。

又由于数据是随机分布没有顺序，所以也不能用从中间位置访问。

那么此时随机位置开始就是最好的选择。

为什么是随机，而不是随意指定。随意指定也是随机的一种，不过随意指定主观性太强，随机算法可以得到更好的结果。

实际计算机上产生的各种随机数并不是真正的随机数，只是伪随机数，不过这不影响数据的计算。

3.2.方向

查找第一个数据如果满足条件自然最好，大部分场景下，第一个数据都是不满足要求的，需要向某个方向搜索前进。

3.2.1.一个方向

从第一个位置开始查找，或者从最后一个位置，行进的方向都是确定的：

• 从第一个位置开始就是从前向后行进。

• 从最后一个位置开始就是从后向前行进。

3.2.2.两个方向

从中间位置开始就存在是向左边行进还是向右边行进的问题。

在一个方向行进时，方向是确定的，没有判断条件。向两个方向行进时，必须有评估函数决定向左还是向右，对于二分算法的评估函数就是排列顺序，如果目标对中间值大或小决定了数据是向左或向右行走。

3.2.3.三个及以上的方向

无论向一个方向或者向两个方向前进，本质都是在一维空间的前进，方向数量有限。

而在三个或以上方向的行进，就是在二维、三维或更高维特征空间的行进。需要将高维空间的行进转化为一维空间的行进才可以。

如果没有足够支撑决策的数据支持，随机指定方向是不差的办法。（没有更好的办法，只能如此） 

设想，把小明蒙眼丢到草原上探险，小明口渴需要找水源，最优的情况是小明熟悉地理环境，可以直接找到水源。如果这里完全陌生，在三维世界里，他有东西南北四个正方向和正方向组成的各种夹角方向，小明如果不想被渴死，肯定要随机选一个方向找水。

3.3.步长

已知两个计算公式：路径/速度=时间；步长*步频=速度。

一组确定的数据，相当于路径是确定，如果需要快速完成任务，需要提高速度。

速度是步长和步频的积，对于同一台计算机，计算机的频率是确定的，那么决定速度的就是步长。

综上，不同算法的速度最终由算法移动的步长决定的，步长越大，代表可以跨过的数据越多，速度自然越快。

3.3.1.固定步长

使用按照顺序逐个检查元素的方式查询数据，步长是确定的就是1，1代表1个元素。

3.3.2.动态步长

使用二分法检查元素，步长是变动的。如果数据长度为100，那么：

• 第一次查找，步长=100/2=50

• 第二次查找，步长=50/2=25

3.3.3.人工调整步长

前两种步长都是比较常见，人工调整步长主要在机器学习中使用。之所以需要人工调整，是因为不同的数据分布不同，需要机器学习工程师根据经验选择一个步长，根据数据收敛的速度微调步长长度。

比如：在基因算法中，在计算初期，因为需要对大量数据计算，就需要使用大步长以期实现快速收敛。如果发现数据目标值一直在来回跳动时，需要调整为小步长。

道理也简单，如果让你从北京到上海，最好坐飞机或高铁，速度快（对应于上文的大步长），如果让你到楼下取快递，肯定步行就足够了（对应于上文的小步长）。

3.4.评估

前文讲到查找行为有三个决策点：

• 当前数据是不是我想要的？

• 如果是或不是，要不要继续查找？

• 如果需要查找，需要查找向哪个方向查找？

以上决策，都需要评估函数，评估函数有两种情况。

3.4.1.单目标评估

单目标评估是最简单的评估方式，符合条件就向指定分支中行进。

3.4.2.多目标评估

多目标评估是多个单目标评估的复合，目标越多计算越复杂。在软件程序中单个程序片段，最好是单目标，过多目标复合在一起会让计算行为非常复杂。

3.5.停止

3.5.1.自动停止

最好的结果是快速查找到数据，代码自动执行完毕，此为主动停止。主动停止也是分为两种情况，比如派出多个小分队取找水源，会存在多个小分队，部分小分队主动停止，其余小分队继续寻找的场景。

3.5.2.被动停止

被动停止，比如时间过长被代码执行人主动放弃执行代码。

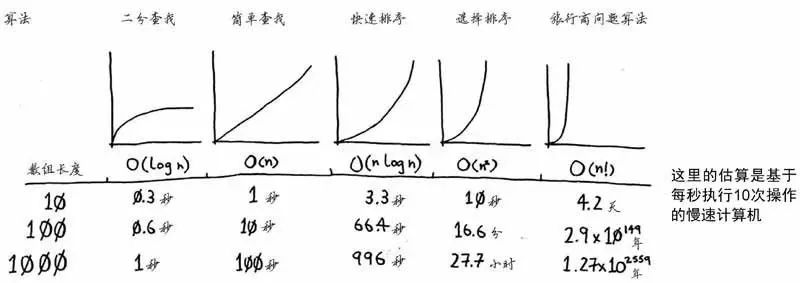
4.时间复杂度

时间复杂度是描述算法的运行时间随规模增长的量度。反映了随着数据量的增长，查找指定数据需要的步数的增长趋势。

注意：这里讲的是步数，不同算法即使步数相同，步长也未必相同。比如：

• 假设成年人的平均步长为0.7米，走完100米，需要143步。

• 儿童的平均步长为0.5米，走完100米，就需要200步。

常见的复杂度函数示意图如下：