计算思维是将生活中的问题编码成计算机可执行的程序，可以由计算机自动执行并得到结果。

• 编码成计算机程序本质就是抽象成数学模型。

• 系统自动执行就是实现自动化。

抽象和自动化正是计算思维的本质。实现计算机自动执行，必然需要使用算法，那么算法从哪里来，如何优化算法呢？

1. 算法概述

1.1. 算法从哪里来

算法从生活中，从已积累的各个学科的知识中来。虽然我们学习算法都是从算法书上直接学习，我们是学习前人已经发明的算法，前人通过生活或其他学科在相同特征场景下，大自然或人类采取的策略获得启发，经过小心推理和验证而发明出新的算法。

比如：“退火算法”、“遗传算法”、“爬山算法”、“贪心算法”、“动态规划”从这些流行算法的名称可以看出这些算法的都受到其他学科的启发。

我们生活在三维世界中，身边相同算法的事物分布相对稀疏。而如果把三维世界的各种要素放在N维的特征空间观察，同样场景会很多相似的对象。这些对象在特征空间里运动，通过观察相似特征空间的其他对象的运动可以获得策略启发。

比如，飞机和小鸟，从三维空间里观察，两者差异巨大，“距离”很远，从特征空间里看，他们相似度要近的多。人敢于想象飞向天空，就是受到鸟类的启发，虽然现在很多飞机并未直接使用仿生学，但是如果没有鸟类的启发，人类可能不会有翱翔天空的梦想。

1.2. 算法如何优化

以一维排序算法为例：

• N个元素，理论上有N×（N-1）×（N-2）× *** ×2×1种组合，排序无论是正序或者倒序就是从N！个组合中选择唯一的组合。

• 排序动作抽象为计算机语句就是：循环、判断、交换。

算法的优化就是用尽可能少的循环次数、判断次数和交换次数，完成从N！中选出指定序列的任务。

不同算法的复杂度可以用大O函数描述，该函数可以刻画算法的时间和空间复杂度。
在不引入分组优化的场景下，大O函数，可以用多项式函数f(x)=axn-1+…+cx+d模拟。

• 如果仅有一次循环，很可能算法的复杂度为O(N)

• 如果有两个嵌套循环，很可能算法的复杂度为O(N²)

• 如果有三个嵌套循环，很可能算法的复杂度是O(N³)

我们知道指数函数增长的非常快，所以如果使用复杂度为指数函数的算法，数据量增长后，算法很快就不堪重负。

指数函数增长快，那么指数函数的反函数对数函数自然增长就慢。如果对多项式函数的x或x^n可以用x=logN的对数函数作为子函数就可以降低函数的复杂度。x=logN作为子函数，就需要有一定的数据结构支撑这样的转化，事实上这种方案是存在的，转化后的复杂度可以为O(logN)。

1.3. 优化算法和机器学习的优化解

机器学习是使用各种算法，在数据特征空间中，找最优解或可接受的解。
人工开发算法，也是在特征空间，找最优的算法。两者也有区别：

• 机器学习的特征空间是基于传感器自动或人工手动采集数据构建的。计算机在人工优选的算法指挥下计算模型并处理数据。

• 人工学习的特征空间是基于自身经历和对前人知识的吸收构建的。

• 人工学习是从前人的结论中学习，而不是从原始数据中挖掘，人工学习的成就不仅取决于知识输入量，更取决于世界观和价值观，人工得出结论与机器得出结论使用的特征空间并不完全重合。

• 对于复杂问题，两者都有天时，有一定的偶然性。

2. 三种排序算法的可视化

冒泡、选择、插入是常见的排序算法，下文将三者排序过程可视化。快速算法未可视化，但是下文会讨论。

2.1. 冒泡算法

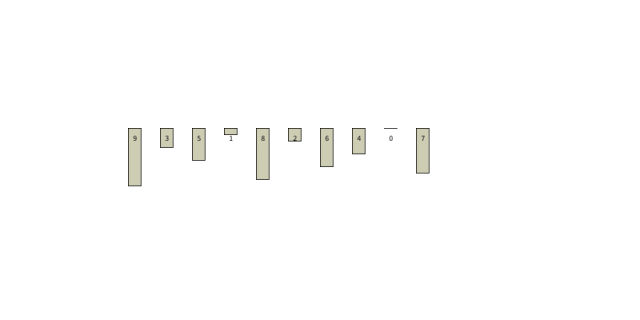
2.2. 选择算法

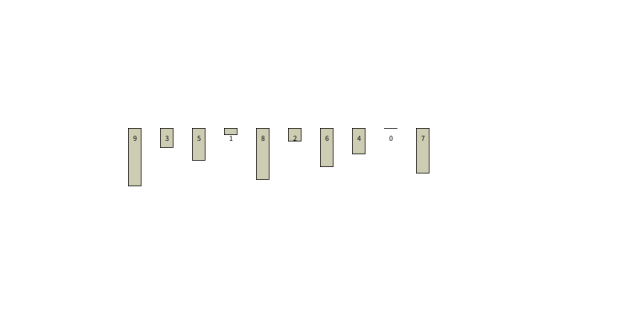
2.3. 插入算法

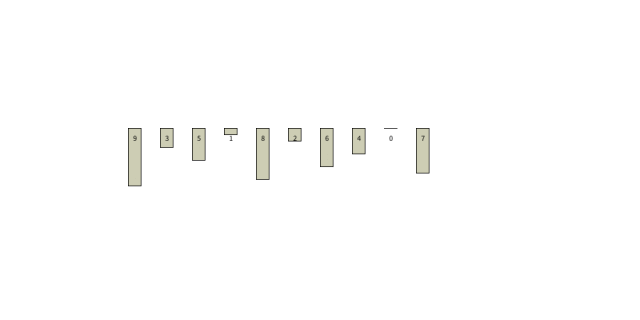
3. 算法分析

排序就是按照大小排列，大小是比较的结果，有比较才有大小，和哪个比较呢？上述四个算法在选择参照物时，采取了不同的策略。

3.1. 动态临近比较

冒泡算法的特点是，每次运算没有固定的参照，只和后面的比较，参照系在每个循环体中都会变化。

但是因为该算法实现了数据大小与左右方向的映射，所以通过多次的积累，最终也可以完成排序。

观察动画中数字7可知，此算法在左侧数据已经排序的条件下，仍然按部就班的逐个比较，逐个移动。

直观上也可发现，此算法的移动次数有可压缩的空间。该算法是中规中矩的算法，算法复杂度为O(N²)。

3.2. 最值比较

排序自然有最大值，最小值，不同于冒泡算法的临近比较，选择算法和插入算法是从头部或尾部开始，选择头部或尾部的值作为参照物比较，使用该值与其余所有元素比较，选出最值。

冒泡算法内循环一次的结果是不确定的，并没有确定任何一位的值，信息增益较慢，而最值比较，一个周期可以确定一个最值，下个周期就可以减少一次循环。最值比较之所以可以减少循环次数，就是因为他循环一次有了明确的信息，信息混乱度已经降低。

在每次循环中，最值确定后，原位置的数据如何处理，选择算法和插入算法选择了不同的策略。

策略一：当前值与最值交换
选择算法使用该策略：该方式会打乱原数据未分类部分的顺序。
策略二：将值插入到最值后面 插入算法使用该策略：该方式较少打乱未分组数据的原顺序。

从上文描述可知，在算法的运算过程中，数据自动分为两组，已分类的组，未分类的组。

选择策略和插入策略的注意力都仅在已分类组，对于未分类组，采取的策略比较简单：选择算法直接放到原最值的位置，插入算法的策略是将值放在最值后面的空格里。

第一种策略，会打乱未分组数据的原顺序，如果元数据有秩序，使用该方案会让原顺序由部分有序变成乱序，要依靠后续的动作矫正。

第二种策略，较少打乱未分组数据的原顺序。两种策略的表现优劣与原数据的混乱程度有关。如果原数据是随机分布，插入算法表现会略好。如果原数据是倒序分布，选择算法表现会更好。

3.3. 选择任意值

通过分析上述三个算法，可知：

冒泡算法，执行时未对信息分组，也可以说相邻两两分组，信息增益较慢。

选择算法和插入算法隐式对数据分为已排序和未排序两组，但是对未排序分组数据的处理并未充分利用循环减少数据混乱度。

快速算法是对数据显式分组。任意选择一个数作为数据基准。一般而言任意选值，每次都选中最值的概率较低。相对于最值只有一个方向对数据分类，选择任意值为基准，可以实现大于和小于该基准的值分布在基准两侧，通过递归多次操作，可以较好的完成数据的排序且常规情况下算法复杂度为O(logN)。

4. 思路拓展

通过尽可能的将业务逻辑放在较少的循环中来降低算法复杂度，作为通用的理念，在以下场景中被发扬光大。

• Java8的Stream接口

• Python的Pandas数据分析接口

Stream和Pandas都是处理大数据的强大工具，两者有一个共同的设计理念，通过降低循环，降低算法复杂度。通过Stream和Pandas包装的函数接口，即实现了对业务思路的表达，也可以将值的运算区分是惰性求值和及早求值。惰性求值可以可以减少循环的次数。